Analyzing survey results, in most cases, means more than just merely comparing two numbers or graphs. While it takes no particular wisdom to decide whether two numbers are different, learning whether that difference is statistically significant requires a bit more skill and effort. This is where t-tests kick in.
Before I show you how to conduct a t-test and how to use Microsoft Excel as a t-test calculator, let’s just briefly explore the origin of this type of tests.
How a Guinness Genius Left a Legacy in Statistics: The Origins of the T-Test
Did you know that one of the most used statistical tests, the t-test, was developed by a beer brewer?
Okay, a beer brewer might be an understatement for an Oxford University graduate of chemistry and mathematics, William Sealy Gosset, but the fact is that this chemist did start his career as an apprentice brewer at the Dublin’s Guinness brewery.

At the time, Guinness started employing scientist brewers so as to find a way to produce large quantities of beer, while maintaining the quality standards. Gosset developed the t-test as a cost-effective way to monitor the quality of stout and make well-informed decisions about which ingredients to use in what amount.
His statistical method for dealing with small sample surveys was accepted by the journal Biometrika. There, he published his paper titled The Probable Error of a Mean in 1908, under the pseudonym “Student” because the Guinness policy didn’t allow their chemists to publish findings at the time. To this very day, Student’s t-distribution theory is considered as one of the cornerstones of contemporary statistics.
Why was it so revolutionary? Well, until Gosset developed his t-test formula, statistics mostly relied on large-sample methods, where you usually needed 150 or more samples to make it work. His theory made it much easier for companies such as Guinness to test new products or product changes on smaller samples so as to save money.
This was a brief story about the origin of the Student’s t-test, one of the fundamental statistical methods still widely used in modern statistics. But where can you use t-tests exactly?
What Are T-Tests Used for
The t-test is used to compare two means (averages) in order to find out whether they are different, and if so, how significant the difference is. It also helps you determine whether those differences could’ve occurred by chance.

A t-test could be used, for example, to compare the GPA of boys and girls to see if there’s any significant difference in average grades depending on gender. In that case, we would have one independent variable (gender) that can have only two values (male and female) and one dependent variable (GPA) that can have many different values (up to 5.00).
You can also use t-tests to analyze the results of a customer satisfaction survey, customer effort score, NPS (Net Promoter Score), or a variety of Likert scale based questions.
There are 3 different types of t-tests, each of which is calculated using a different t-test equation (we’ll show you how to use a t-test calculator a bit later)
Different Types of T-Tests (Including T-Test Formulas)
1. One-sample t-test
This type of t-test examines whether the mean (average) of data from one group differs from the pre-specified value.
2. Two-sample t-test
This type of t-test helps you decide whether the means (averages) of two separate groups of data significantly differ from one another.
3. Paired t-test
A paired t-test is used when you survey one group of people twice with the same survey. This type of t-test can show you whether the mean (average) has changed between the first and second time they took the survey.
T-test equations
The table below shows t-test formulas for all three types of t-tests: one-sample, two-sample, and paired.

How to Conduct a Two-Sample T-Test (T-Test Calculator Explanation Included)
There are 4 steps to conducting a two-sample t-test:
1. Calculate the t-statistic
As could be seen above, each of the 3 types of t-test has a different equation for calculating the t-statistic value. Here’s the formula for a two-sample t-test:
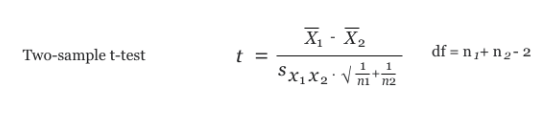
Where:
- t is the t-statistic
- x1 is the mean value for sample 1
- x2 is the mean value for sample 2
- n1 is the number of people from the 1st sample who provided a response to the survey
- n2 is the number of people from the 2nd sample who provided a response to the survey
- sx1x2 is the standard deviation
The standard deviation (sx1x2) is calculated in the following way:
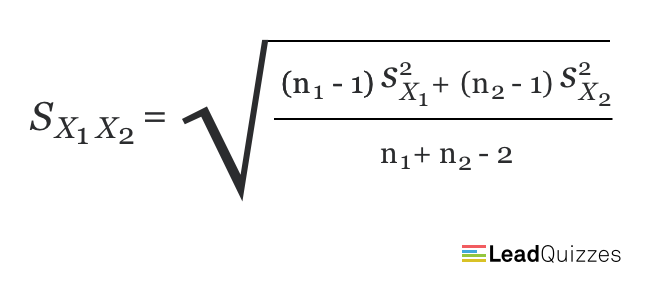
Where:
- sx1 is the standard deviation for sample 1
- sx2 is the standard deviation for sample 2
2. Calculate the degrees of freedom
Degrees of freedom is the number of independent pieces of information that were taken into account when calculating the estimate. It’s not the same as the number of independent items in a sample. In order to calculate the degrees of freedom, all you need to do is subtract 1 from the total number of items in the sample. For example, if you had 10 people in one sample group that had taken your survey, the df would be 10 – 1 = 9.
Since we are conducting a two-sample t-test here, the df formula is slightly different (as we have two samples instead of one). Here it is:
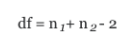
Degrees of freedom (df) is basically the number of different ways a mean could vary.
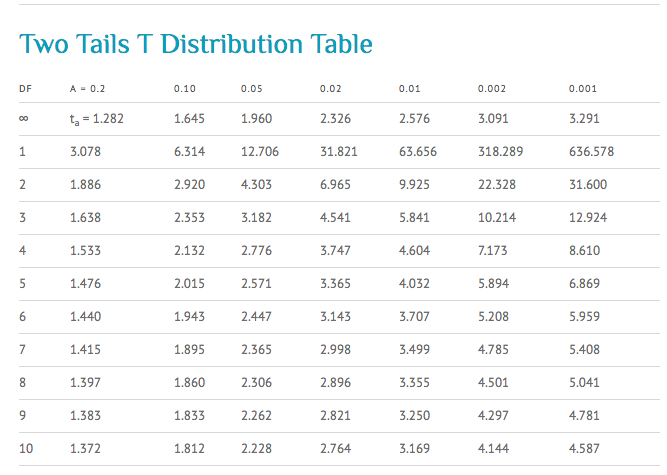
3. Determine the critical value
The critical value represents the threshold at which the difference between the two values should be considered statistically significant. You can find the critical value in the t-distribution table, using the degrees of freedom you calculated in the previous step.
If there’s no specified alpha level, you should use 0.05 (5%). Keep in mind that most analysts nowadays use a two-tailed t-test instead of a one-tailed one.
4. Compare the t-statistic value to critical value
If the t-statistic you obtained using our formula above (step 1) is greater than the critical value you found in step 3, the statistical difference may be considered significant. If your t-statistic is lower, then the difference between the two numbers is statistically insignificant.
T-Test Calculator: How to Perform a T-Test in Microsoft Excel
To perform a t-test in Microsoft Excel, we’re going to utilize the Data Analysis plug-in. Here’s how you can do it in just a few simple steps.
Step 1: Install the Data Analysis plug-in
It’s quite simple to install the Data Analysis plug-in if you don’t already have it in your Microsoft Excel. To do this, just navigate to ‘File > Options‘ and in the new window, click on ‘Add-ins‘. A new window like this with available add-ins will open:
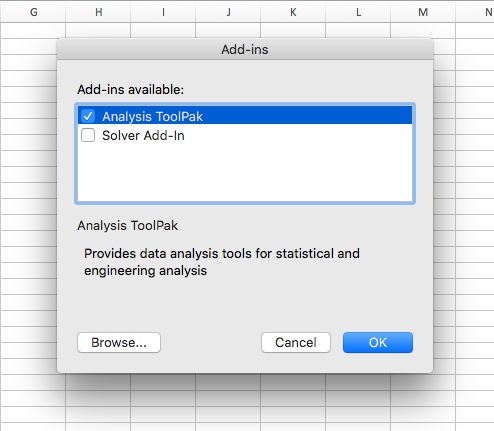
Here you should select “Analysis ToolPak” and click OK. You should now be able to find the Data Analysis option under ‘Data > Data Analysis‘:
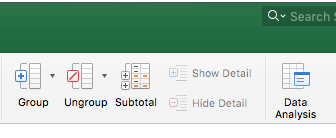
Using the Data Analysis plug-in to perform t-tests
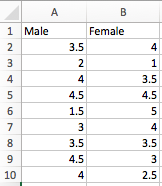
To conduct a t-test in Microsoft Excel, you should first create two columns with different data. Each column should list the values for each separate sample group. If we go back to our GPA example, you should create one column labelled “Male” and another one labelled “Female” and list there all of their GPA scores. This is how such a table looks in Excel:
Next, navigate to ‘Data > Data Analysis’ and click on the Data Analysis button. Once you do that, a new window containing a list of the Analysis Tools will open, where you should be able to find and select the right t-test method for your needs.
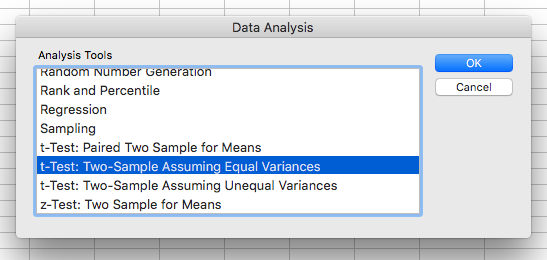
After you click OK, a new window will open where you are expected to select the cell range for each of the groups. Also, here you should select the alpha (level of significance) you’re going to use – it’s usually set at 0.05 (5%).
Output options allow you to choose where you want your results to be shown. In my example, I have simply set the ‘Output Range’ to an empty cell in the existing sheet.
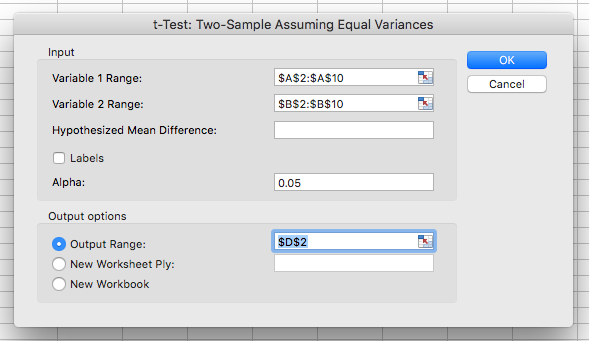
Click OK and Excel will generate a report like this one:
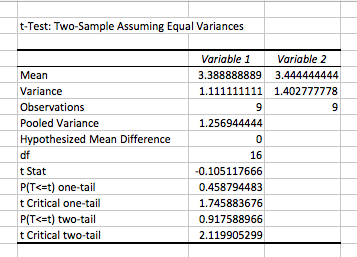
As shown above, the output created by our t-test calculator shows various data such as mean, variance, degrees of freedom (df), t-statistic, p-value, and more. How can you interpret the results above (if you’re not a statistician)?
In my example above, the null hypothesis was: “There is no difference in GPA between male and female students.”
The alternative hypothesis was: “There is a difference in GPA between male and female students.”
As it was not pre-specified which group has a higher or lower GPA than the other, we should examine the output for the two-tail analysis. We can see in the table that the P-value for the two-tail analysis is 0.917588966, which is higher than our alpha level of significance (P>0.05). Therefore, we accept the null hypothesis as true.
Even though I’ve tried to simplify things here (as much as possible) to make them more accessible to the general audience, marketers and other non-professional survey-makers, conducting t-tests, setting up and using a t-test calculator, and analyzing the survey results this way can still be quite difficult and confusing. At least if you don’t have a strong background in statistics or mathematics.
Still, unlike using t-tests to analyze the survey results, creating those surveys doesn’t have to be difficult nor time-consuming. Just click on the image below and create your survey within minutes!